直角三角形的三边关系是三角形中最基本、最重要的关系之一。在直角三角形中，最长的边被称为斜边，而其余两边被称为直角边。

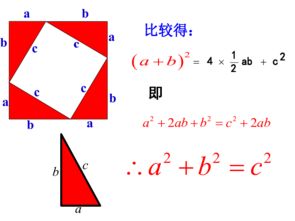
    这个定理的证明过程非常有趣，它涉及到几何和代数两个领域。在几何上，可以通过将斜边和其中一个直角边作为对角线，构造一个正方形，然后利用正方形的性质来证明。而在代数上，可以通过展开平方并利用加法交换律和结合律来证明。

    特殊情况：当直角三角形的两直角边长度相等时，它是一个等腰直角三角形。在这种情况下，斜边等于两直角边的平方根之和，即 c = √(a2 + b2)。

    应用：勾股定理在几何学、物理学、工程学等多个领域都有广泛的应用。例如，在建筑学中，可以用它来计算建筑物的稳定性和安全性；在物理学中，可以用它来计算与直角三角形相关的力和位移；在工程学中，可以用它来设计桥梁、建筑和其他结构。

探索直角三角形三边关系：黄金分割与勾股定理的奇妙结合

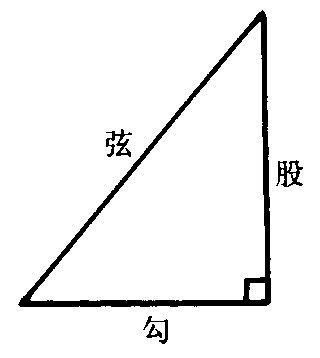
    直角三角形，作为我们日常生活中常见的几何形状，不仅在建筑、艺术等领域有着广泛的应用，还蕴含着许多深奥的数学秘密。今天，我们就来深入探讨一下直角三角形三边关系中的奇妙之处，看看黄金分割与勾股定理如何在这里交织出一幅美丽的数学画卷。

一、黄金分割与勾股定理的起源

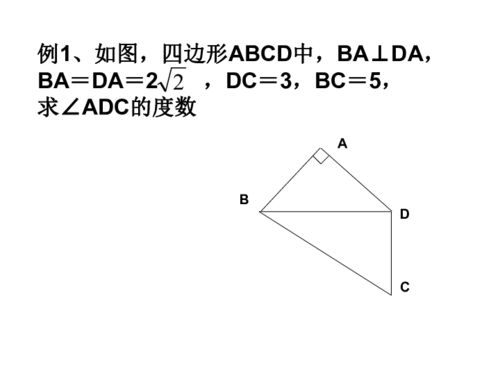
    黄金分割，又称黄金比，最早出现在古希腊数学家欧几里得的几何原本中。它表示在一个线段上，较长的部分与较短的部分之比等于整体与较长部分之比，这个比例约为1.618:1。而勾股定理，则是在直角三角形中，直角边的平方和等于斜边的平方，这是古希腊数学家毕达哥拉斯的重要发现。

二、直角三角形三边关系中的黄金分割

    在直角三角形中，如果直角边的长度分别为a和b，斜边的长度为c，那么根据勾股定理，我们有a2+b2=c2。如果我们进一步观察这个等式，我们会发现当a和b分别为整体和部分时，它们的比例正好是黄金分割的比例。这似乎是一个巧合，但实际上，这背后隐藏着更深层次的数学原理。

三、黄金分割与勾股定理的奇妙结合

    当我们深入研究直角三角形的性质时，我们会发现黄金分割与勾股定理之间的联系更加紧密。在直角三角形中，如果我们取斜边c的中点d，那么cd的长度就是a和b的平均值。这个平均值就是黄金分割中提到的“部分”，而斜边c就是“整体”。这意味着在直角三角形中，斜边上的中线长度与斜边长度的比值正好是黄金分割的比例。

四、黄金分割与勾股定理的实际应用

    通过以上分析，我们可以看到黄金分割与勾股定理在直角三角形三边关系中有着密切的联系。它们不仅相互依存，还共同构成了丰富多彩的数学世界。在未来，随着科学技术的不断发展，我们相信黄金分割与勾股定理将在更多领域发挥重要作用，为人类社会的发展贡献更多的智慧和力量。