lnx的原函数
文章来源:未知 •
作者:admin •
• 阅读次数:
要找到lnx的原函数,我们可以使用积分的方法。
我们知道lnx的导数是1/x。根据原函数与导数的关系,我们知道如果一个函数的导数是f(x),那么这个函数就是f(x)的原函数加上一个常数C。
因此,我们可以写出lnx的原函数为:
∫lnx dx = xlnx - ∫x (1/x) dx
= xlnx - x + C
其中C是常数。
所以,lnx的原函数是xlnx - x + C。
一、引言

二、原函数定义
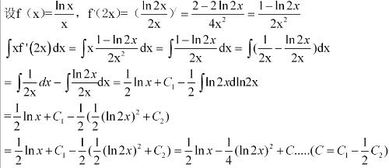
原函数是指一个函数的导数等于另一个给定函数的函数。如果函数F(x)是另一个函数f(x)的原函数,那么F'(x) = f(x)。对于lx,我们需要找到一个函数,其导数等于lx。
三、lx的原函数求解过程

我们需要理解如何求解函数的原函数。一种常见的方法是使用积分,即求解∫f'(x)dx。对于lx,它的导数是1/x。因此,我们需要求解∫1/xdx。
接下来,我们进行积分。积分∫1/xdx的结果是l|x| + C,其中C是积分常数。因此,lx的原函数是l|x| + C。
四、结果表达式
根据上述过程,我们可以得到lx的原函数为l|x| + C,其中C是积分常数。这个结果说明,lx的原函数是一个包含绝对值和常数的对数函数。
五、结论
通过本文的探讨,我们得到了lx的原函数为l|x| + C。这个结果可以帮助我们更好地理解自然对数函数及其性质。在数学和工程领域中,自然对数函数及其原函数具有广泛的应用,因此掌握其原函数的求解方法对于学习和应用都非常重要。
文章来源互联网或者编辑者发布,如有侵权请联系删除。发布者:admin,转载请注明出处:lnx的原函数