反正弦函数图像,探索神秘的反弦函数图像：揭开其背后的数学奥秘

```

y = sin(x)

```

这个函数图像是一个周期函数，它的值域是-1到1，在x轴上方和下方都有对应的图像。当x的值从-π到π变化时，y的值从-1到1变化。在这个周期内，函数图像呈现出正弦波的形状。由于它是周期函数，因此可以在不同的周期内呈现出不同的形状。

对于反正弦函数，它的定义域是-1到1，值域是全体实数。在图像上，它是一个单调递增的函数，随着x的增加，y的值也在增加。在定义域内，函数图像呈现出先下降后上升的趋势。在x=0处，函数值为0，在x=-1和x=1处，函数值分别为负无穷和正无穷。

反正弦函数的图像是一个先下降后上升的曲线，它的值域是全体实数，定义域是-1到1。

探索神秘的反弦函数图像：揭开其背后的数学奥秘

在数学的世界里，有很多奇妙的函数图像，其中反弦函数图像因其独特的性质和美感，吸引了无数数学爱好者的目光。本文将带您一起探索反弦函数图像的奥秘，感受其独特的魅力。

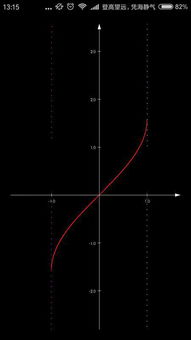
反弦函数，也称为反正弦函数，是三角函数的一种。其定义为：y = arcsi(x)，其中x是正弦函数的值域[-1,1]，y是反弦函数的定义域[-π/2, π/2]。反弦函数具有奇函数和单调递增的性质，这些性质使得反弦函数图像成为一个非常有趣的研究对象。

要绘制反弦函数图像，我们需要确定一个角度范围，通常是-π/2到π/2，并在这个范围内选择一些点，计算其正弦值。然后，将这些正弦值作为输入值代入反弦函数中，得到对应的y值。将这些点连接起来，就可以得到反弦函数的图像。

反弦函数图像是一个非常美丽的曲线，它的形状像一只振翅欲飞的蝴蝶。在图像上，我们可以看到一些有趣的特征，例如对称性、周期性和单调性。这些特征使得反弦函数图像成为数学研究中的一个重要对象。

通过对反弦函数的探索和了解，我们可以感受到数学的无限魅力。反弦函数图像不仅是一个美丽的曲线，还隐藏着许多数学奥秘。通过深入研究和探索，我们可以更好地理解这个神秘的世界，并发现更多有趣的现象和应用。让我们一起揭开反弦函数图像的神秘面纱，感受数学的美妙与力量！

文章来源互联网或者编辑者发布，如有侵权请联系删除。发布者：admin，转载请注明出处：反正弦函数图像,探索神秘的反弦函数图像：揭开其背后的数学奥秘