反三角函数值域,探究反三角函数的值域:超越常规,发现无限可能
文章来源:未知 •
作者:admin •
• 阅读次数:
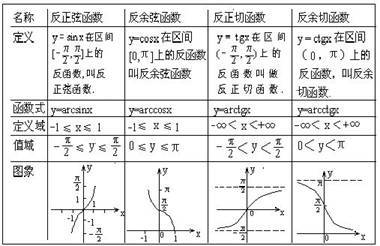
反三角函数的值域如下:
反正弦函数:定义域为[-1,1],值域为[-π/2,π/2]。
反余弦函数:定义域为[-1,1], 值域为[0,π]。
反正切函数:定义域为R,值域为(-π/2,π/2]。
反余切函数:定义域为R,值域为[0,π)。
反正割函数:定义域为(-∞,-1]U[1,+∞),值域为[0,π/2)U(π/2,π]。
反余割函数:定义域为(-∞,-1]U[1,+∞),值域为[0,π/2)U(π/2,π]。
探究反三角函数的值域:超越常规,发现无限可能

在数学的浩瀚海洋中,反三角函数是一颗璀璨的明珠。它们以一种独特的方式描绘了角度与实数之间的关系,展示了一种奇妙的数学现象。反三角函数的值域,更是充满了惊喜与奥秘。让我们一起,深入探究反三角函数的值域,解锁其中的无限可能。
一、反三角函数:角度与实数的奇妙联系

二、反三角函数的值域:超越常规的数学之美
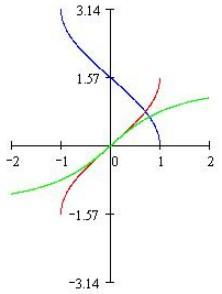
反三角函数的值域是一个广袤而神秘的领域。在这里,我们不仅可以发现数学的美,还能领略到科学的魅力。从0到π的区间内,反三角函数的值域不断变化,展现出丰富多彩的数学形态。而当角度超过π时,反三角函数的值域又呈现出另一种规律。
三、探究反三角函数值域:无限可能的新世界
文章来源互联网或者编辑者发布,如有侵权请联系删除。发布者:admin,转载请注明出处:反三角函数值域,探究反三角函数的值域:超越常规,发现无限可能